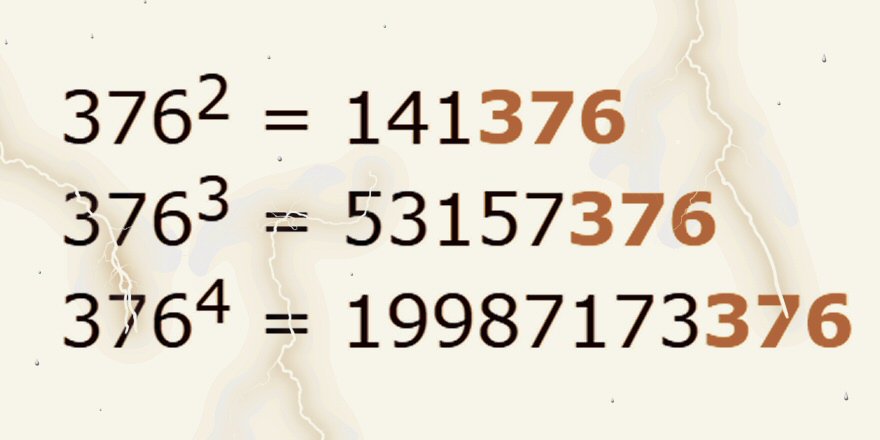فید

14

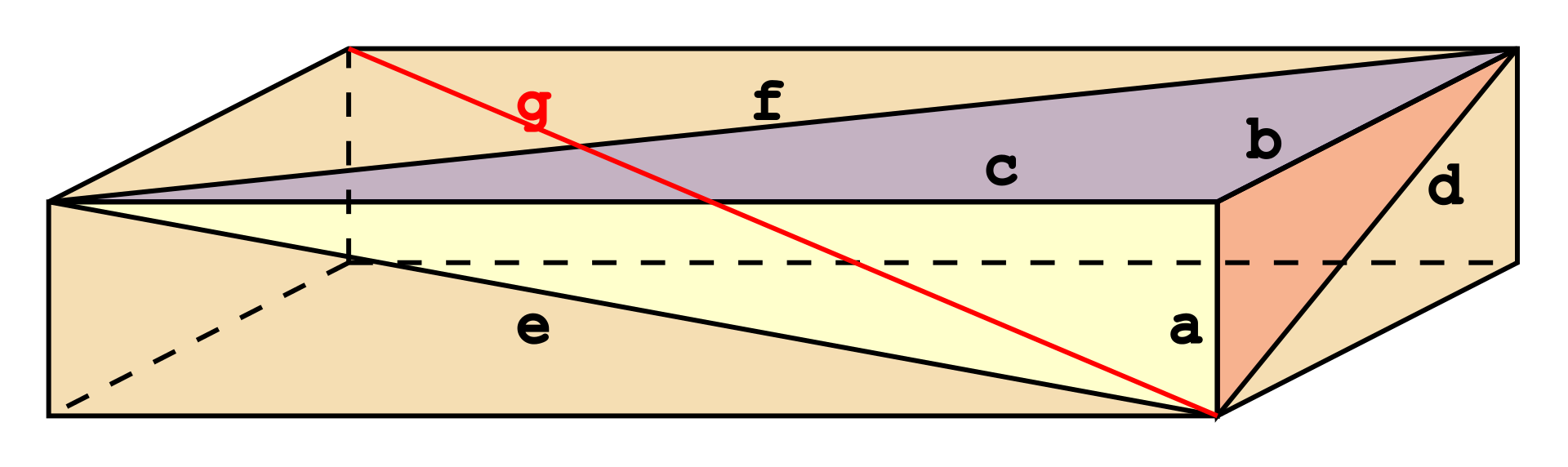
در ریاضیات، آجر اویلر یا مکعب اویلر که به‌نام لئونارد اویلر نامگذاری شده است، مکعبی است که لبه‌ها و تمامی قطر‌های آن اعدادی طبیعی هستند. آجر اصلی اویلر نیز به مکعبی گفته می‌شود که طول‌های آن نسبت به هم اول باشند. 

ابعاد یک آجر اویلر را می‌توان مطابق با پاسخ معادله سیاله زیر در نظر گرفت.

{\begin{cases}a^{2}+b^{2}=d^{2}\\a^{2}+c^{2}=e^{2}\\b^{2}+c^{2}=f^{2}\end{cases}}

در رابطه فوق a,b,c برابر با طول لبه‌ها بوده و d,e,f نشان‌دهنده قطر‌ها هستند. این مکعب‌ها ویژگی‌هایی خاص داشته از این رو از آن در علوم و مهندسی استفاده می‌شود.

کوچک‌ترین آجر اویلر در سال ۱۷۱۹ توسط «پاول هالک» (Paul Halcke) بدست آمد. لبه‌های این آجر برابر است با:

(d,e,f ) = (125, 244, 267)

در ادامه برخی دیگر از مهم‌ترین ابعاد یافته شده به عنوان آجر اویلر نیز ارائه شده‌اند.

(85,132,720) — (157,725,732)

(140,480,693) — (500,707,843)

(160,231,792) — (281,808,825)

(187,1020,1584) — (1037,1595,1884)

(195,748,6336) — (773,6339,6380)

(240,252,275) — (348,365,373)

(429,880,2340) — (979,2379,2500)

(495,4888,8160) — (4913,8175,9512)

(528,5796,6325) — (5820,6347,8579)

آجر کامل

یک آجر کامل، مکعبی اویلری محسوب می‌شود که قطر فضایی آن نیز عددی صحیح است. به عبارتی دیگر معادله زیر نیز باید بین ابعاد اصلی (یا همان لبه‌ها) برقرار باشد. قطر فضایی، قطری است که دو گوشه مخالف مکعب را به هم وصل می‌کند.

{\displaystyle a^{2}+b^{2}+c^{2}=g^{2},}

در رابطه فوق g نشان‌دهنده قطر فضایی است. تاکنون کسی مکعبی کامل را پیدا نکرده و هیچکس نیز هنوز وجود نداشتن مکعب کامل را اثبات نکرده است.

آجر اصلی کامل یا آجر اولیه کامل نیز به مکعبی گفته می‌شود که هم لبه‌ها و قطر‌های وجوه آن، اعدادی صحیح بوده و همزمان نسبت به هم اعدادی اول باشند.

آجر تقریبا کامل

یک مکعب تقریبا کامل، از 7 طول، دارای 6 طول صحیح است. چنین مکعب‌هایی را می‌توان در سه دسته حجمی، طولی یا سطحی تقسیم‌بندی کرد. در مورد مکعب حجمی، طول قطر فضایی عددی گنگ است. در مکعب طولی نیز یکی از لبه‌های a،b،c عددی گنگ خواهد بود.

نویسنده:سجاد اسدی

 

 

26

در ریاضیات به یک عدد زمانی عدد شگفت انگیز گفته می‌شود که n رقم آخر مربع عدد، برابر با خود عدد باشد. برای مثال 625 = 25*25 و 5776 = 76*76. این اعداد به نام اعداد اتومورفیک نیز نامیده می‌شوند.

اعداد اتومورفیک بزرگ‌تری مانند 212890625  و 787109376 نیز وجود دارند:

2128906252 = 45322418212890625

و

7871093762 = 619541169787109376

همچنین باید بدانید که اگر n رقم آخر مربع عدد برابر با خود عدد باشد، این رابطه در مورد مکعب عدد و توان‌های بالاتر نیز صدق می‌کند. مشخص شده است که برای هر n>1 دو عدد شگفت انگیز به طول n وجود دارد.

حتی یک فرمول نیز برای این دو عدد وجود دارد. فرمول نخست به صورت باقیمانده 5 به توان 2n تقسیم بر 10nاست و دومی به صورت 10n + 1 منهای اولی است.

نویسنده:سجاد اسدی

 

بیشتر ببینید